Série 3:
Structures de contrôle et expressions logiques

Buts

Le but de cette série est de vous faire travailler avec les structures de contrôle de Java: l'instruction conditionnelle if et les boucles for, while et do..while. Vous vous familiariserez également avec la manipulation d'expressions logiques. Notez que pour les exercices qui ne vous demandent pas de produire du code Java, il n'est pas nécessaire d'utiliser Eclipse (par exemple pour l'exercice 4). Pour les autres, vous procéderez comme d'habitude, en créant un projet pour la série.

Exercice 1: Résolution de polynômes de degré 2 (-, Niveau 0)

Nous voulons écrire un programme permettant de trouver les zéros de polynômes de degré 2 de la forme ax2+bx+c, où les coefficients sont des nombres réels et a est non nul (sans quoi ce ne serait plus un polynôme de degré 2...).

  1. Commencez par ouvrir le fichier (vide) Degre2.java dans votre éditeur favori ou dans Eclipse.
  2. Préparez la "coquille vide" de base accueillant votre programme : 

    class Degre2 {

    public static void main(String[] args) {
    }
}

    Nous verrons plus tard dans le cours à quoi correspondent exactement toutes ces lignes, mais pour l'instant considérez cela comme la base minimale pour que votre programme fonctionne.

    On peut maintenant commencer à attaquer notre problème.

  3. Commençons donc par prévoir la place pour les trois coefficients de notre polynôme : a, b et c. Il faut pour cela déclarer des variables.

    Comme nous souhaitons que ces coefficients soient des nombres réels, nous déclarons des variables de type double  : 

    class Degre2 {

    public static void main(String[] args) {
        double a;
        double b;
        double c;
    }
}

    Note : on aurait aussi pu écrire en une ligne 

    double a,b,c;

  4. Maintenant, le réflexe du bon programmeur : il faut penser à initialiser ces variables. Il nous semble ici naturel de les initialiser à zéro : 

    class Degre2 {

    public static void main(String[] args) {
        double a = 0.0;
        double b = 0.0;
        double c = 0.0;
    }
}

  5. Il faut ensuite récupérer les valeurs des paramètres entrés par l'utilisateur. Étant donné que a ne doit pas être nul, nous allons utiliser une boucle dans laquelle nous vérifierons cette condition. Nous pouvons ensuite acquérir les paramètres b et c. 

    import java.util.Scanner;

class Degre2 {

    private static Scanner scanner = new Scanner(System.in);

    public static void main(String[] args) {
        double a = 0.0;
        double b = 0.0;
        double c = 0.0;

        // tant que a est nul, demander une valeur a l'utilisateur
        while (a == 0.0) {
            System.out.print("Entrez une valeur non nulle pour a :");
            a = scanner.nextDouble();
        }

        System.out.print("Entrez une valeur pour b:");
        b = scanner.nextDouble();
        System.out.print("Entrez une valeur pour c:");
        c = scanner.nextDouble();
    }
}

  6. Maintenant que nous connaissons tous les paramètres de l'équation, nous pouvons la résoudre. Il nous faut tout d'abord calculer le discriminant delta = b*b - 4*a*c.

    Il faut donc prévoir de la place pour le stocker : une nouvelle variable de type double.

    On peut ici choisir de la déclarer sans initialisation puis de lui affecter la bonne valeur à l'aide d'une autre instruction ou plus simplement de l'initialiser directement avec b*b - 4*a*c puisque toutes ces valeurs sont connues à ce stade là. C'est cette seconde solution qui est choisie ici : 

    import java.util.Scanner;

class Degre2 {

    private static Scanner scanner = new Scanner(System.in);

    public static void main(String[] args) {
        double a = 0.0;
        double b = 0.0;
        double c = 0.0;

        // tant que a est nul, demander une valeur a l'utilisateur
        while (a == 0.0) {
            System.out.print("Entrez une valeur non nulle pour a :");
            a = scanner.nextDouble();
        }
        
        System.out.print("Entrez une valeur pour b:");
        b = scanner.nextDouble();
        System.out.print("Entrez une valeur pour c:");
        c = scanner.nextDouble();
        double delta = b * b - 4.0 * a * c;
    }
}

  7. Pour le calcul de la solution, différents cas peuvent se produire en fonction de la valeur prise par le discriminant, que nous distinguons dans le programme à l'aide de blocs if-else :

    La méthode Java permettant de calculer des racines carrées s'appelle sqrt(), qui vient de l'anglais "square root".
    Il est possible d'utiliser cette méthode (ainsi que d'autres fonctions mathématiques) en précisant la classe (Math) à laquelle elle appartient. Ceci se fait au moyen de la notation Math.sqrt() que nous comprendrons lorsque nous aurons abordé la programmation orientée-objet.

    Le programme complet devient donc : 

    import java.util.Scanner;

class Degre2 {

    private static Scanner scanner = new Scanner(System.in);

    public static void main(String[] args) {
        double a = 0.0;
        double b = 0.0;
        double c = 0.0;

        // tant que a est nul, demander une valeur a l'utilisateur
        while (a == 0.0) {
            System.out.print("Entrez une valeur non nulle pour a:");
            a = scanner.nextDouble();
        }
        
        System.out.print("Entrez une valeur pour b:");
        b = scanner.nextDouble();
        System.out.print("Entrez une valeur pour c:");
        c = scanner.nextDouble();
        double delta = b * b - 4.0 * a * c;
        if (delta < 0.0) {
            System.out.println("Pas de solutions reelles");
        } else if (delta > 0.0) {
            System.out.println("Deux solutions : "
                        + (-b - Math.sqrt(delta)) / (2.0 * a)
                        + " et " + (-b + Math.sqrt(delta)) / (2.0 * a));
            
        } else {
            System.out.println("Une solution unique : " + -b / (2.0 * a));
            
        }
    }
}


Exercice 2: MOOC (cours en ligne) (MOOC, Niveau 1)

Pour préparer le cours du mercredi 25.9.2024, vous pouvez, après avoir visionné les vidéos en lignes de la semaine 2 et de la semaine 3 de MOOC, répondre aux quiz des mêmes semaines : quiz de la semaine 2 et quiz de la semaine 3.

Exercice 3: Quand c'est pas pair c'est impair (if, Niveau 1)

Ecrivez un programme Java qui lit un nombre entier et indique s'il est positif, négatif ou s'il vaut zéro et s'il est pair ou impair.
Exemple d'exécution: 
Entrez un nombre entier : 5
Le nombre est positif et impair

Entrez un nombre entier : -4
Le nombre est négatif et pair

Entrez un nombre entier : 0
Le nombre est zéro (et il est pair)

Exercice 4: Dans l'intervalle ... ou pas (if, expressions logiques, Niveau 2)

Soit I = [2,3[ U ]0,1] U [-10,-2] dans l'ensemble des réels.

écrivez le programme Intervalle.java qui :

  1. demande à l'utilisateur d'entrer un réel ;
  2. enregistre la réponse de l'utilisateur dans une variable x de type réel ;
  3. teste l'appartenance de x à l'ensemble I et affiche le message «x appartient à I» si c'est le cas, et «x n'appartient pas à I» dans le cas contraire. Ce test doit utiliser uniquement les opérateurs relationnels < et ==. Tous les opérateurs logiques sont, par contre, autorisés.

Notez que, en logique élémentaire, «non(A et B)» peut aussi s'écrire «(non A) ou (non B)».

Testez votre programme avec les valeurs -20, -10, -2, -1, 0, 1, 1.5, 2, 3 et 4.

Voici à quoi devrait ressembler l'exécution de votre programme : 

Entrez un nombre decimal : -20
x n'appartient pas a I
...

Entrez un nombre decimal : -10
x appartient a I
...


Entrez un nombre decimal : -2
x appartient a I
...


Entrez un nombre decimal : -1
x n'appartient pas a I
...


Entrez un nombre decimal : 0
x n'appartient pas a I
...


Entrez un nombre decimal : 1
x appartient a I
...

Entrez un nombre decimal : 1.5
x n'appartient pas a I
...

Entrez un nombre decimal : 2
x appartient a I
...

Entrez un nombre decimal : 3
x n'appartient pas a I
...


Entrez un nombre decimal : 4
x n'appartient pas a I
...


Exercice 5: On tourne en rond (Boucles, Portée, Niveau 1)

Exercice 5.3.1

Indiquez l'affichage de chacune des boucles for suivantes. Exécutez dans un terminal le programme BouclesFor.java pour vérifier vos réponses (Tapez "Enter" pour passer d'une boucle à la suivante). Les boucles infinies éventuelles peuvent être interrompues en tapant <ctrl-c> dans le terminal ou encore, si vous exécutez ce code dans Eclipse/IntelliJ, en cliquant sur le petit carré rouge dans la vue "Console". 

// Exemple 1
for (int i = 0; i < 5; i++) {
    System.out.print(i + " ");
}

// Exemple 2
for (int i = 3; i <= 8; i++) {
    System.out.print(i + " ");
}
        
// Exemple 3        
for (int i = 2; i > -2; i--) {
    System.out.print(i + " ");
}
        
// Exemple 4
for (int i = 0; i > 5; i--) {
    System.out.print(i + " ");
}
        
// Exemple 5
for (int i = 0, j = 5; (i <= 10 && j < 7); i++, j++) {
    System.out.print(i + " " + j + " * ");
}

// Exemple 6
for (int i = 0, j = 5; i <= 10 || j < 7; i++, j++) {
    System.out.print(i + " " + j + " * ");
}
        
// Exemple 7
boolean b = true;
for (int i = 3; b; i++) {
    System.out.print(i + " " + b + " * ");
    b = (i < 6);
}
        
// Exemple 8
for (int i = 0, j = 6; i != j; i++, j--) {
    System.out.print(i + " " + j + " * ");
}
        
// Exemple 9
for (int i = 0; i < 3; i++) {
    System.out.print(i + " ");
    for (int j = 0; j < 3; j++) {
        System.out.print(j + " ");
    }
    System.out.print(" * ");
}
        
// Exemple 10
for (int i = 3; i < 15; i--) {
    System.out.print(i + " ");
}

Exercice 5.3.2

Indiquez ce qui sera affiché par chaque partie de code ci-dessous. Exécutez dans un terminal le programme AffichageBoucles.java pour vérifier vos réponses (ce programme affichera le résultat pour toutes les boucles d'un seul coup, contrairement au précédent). 

// Exemple 1
int n = 5;
int a = 2;
for(a = 3; a < n + 1; a = a++) {
    System.out.println(a-1);
    a = a + 1;
}

// Exemple 2
int n = 3;
int b = 5;
while (b <= 4 * n) {
    System.out.println(b);
    b = b * 2;
}
System.out.println(b);

// Exemple 3
int n = 3;
int c = 6 * n;
do {
    c = c - n * 2;
    System.out.println(c);
} while (c >= 0);
System.out.println(c);

// Exemple 4
int n = 3;
int d = 3;
while (d < n) {
    d = d + 1;
}
System.out.println(d);

// Exemple 5
int n = 3;
int e = 3;
do {
    e = e + 1;
} while (e < n);
System.out.println(e);

// Exemple 6
int n = 3;
int f = 3;
for (f = 0; f < n; f = f + 1);
    System.out.println(f);

Exercice 5.3.3

Expliquez pourquoi les deux portions de code suivantes ne compilent pas en Java : 

// Exemple 1
int i = 0;
for (int i = 1; i < 5; ++i)
    System.out.println(i);

// Exemple 2
for (int i = 0; i < 5; ++i);
    System.out.println(i);

Exercice 5.3.4

Complétez le programme BouclesEquivalentes avec une boucle while et une boucle do..while qui font la même chose que la boucle for déjà présente dans le programme. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
 
class BouclesEquivalentes {

    public static void main(String[] args) {
        System.out.println("Boucle for :");
        for (int a = 3; a <= 10; a++) {
            System.out.println("a : " + a);
        }

        System.out.println("Boucle while :");
        // A compléter. Ecrivez une boucle while qui fait la même chose
        // que la boucle for ci-dessus 

        System.out.println("Boucle do..while :");
        // A compléter. Ecrivez une boucle do..while qui fait la même
        // chose que la boucle for ci-dessus.
    }
}


Exercice 6: Tables de multiplications (for, Niveau 1)

Ecrivez un programme Tables.java affichant les tables de multiplication de 2 à 10.

Votre programme devra produire la sortie suivante à l'écran : 

        Tables de multiplication

Table de 2 :
  1 * 2 = 2
  ...
  10 * 2 = 20
...
Table de 5 :
  1 * 5 = 5
  2 * 5 = 10
  ...
...
Table de 10 :
  1 * 10 = 10
  ...

Méthode :

Utilisez deux structures d'itération for imbriquées l'une dans l'autre.


Exercice 7: L'heure du bilan (algorithme, if, boucles, Niveau 2)

Votre tante fortunée vous envoie désormais un montant chaque mois. A la fin de l'année vous souhaitez faire un bilan de vos richesses. Ecrivez le programme Java Bilan.java vous affichant la somme mensuelle moyenne reçue, le montant minimal reçu sur l'année et le montant maximal reçu sur l'année. Le bilan se fera sur n montants de la façon suivante:

Donnez n: ..
Donnez le montant du mois 1 (Frs): ..
Donnez le montant du mois 2 (Frs): ..
Donnez le montant du mois 3 (Frs): ..
...
Il affichera (exemple pour n = 3, montant1 = 100, montant2 = 200 et montant3 = 400):

La somme mensuelle moyenne reçue est: 233 
Le montant mensuel minimal reçu est: 100 
Le montant mensuel maximal reçu est: 400

Exercice 8: Plus Grand Diviseur Commun (Algorithme, if, boucles, Niveau 2)

Ecrivez un programme PGDC.java qui calcule et affiche le plus grand diviseur commun de deux nombres entiers positifs entrés au clavier. Exemples d'exécution du programme:

Entrez un nombre positif :  9
Entrez un nombre positif :  6
Le plus grand diviseur commun de 9 et 6 est 3

Entrez un nombre positif :  9
Entrez un nombre positif :  4
Le plus grand diviseur commun de 9 et 4 est 1
Utilisez l'algorithme d'Euclide pour déterminer le plus grand diviseur. Cette formule se résume comme suit:
Soient deux nombres entiers positifs a et b. Si a est plus grand que b, le plus grand diviseur commun de a et b est le même que pour a-b et b. Vice versa si b est plus grand que a.
Les équivalences mathématiques utiles sont:
  1. Si a > b, alors PGDC(a, b) = PGDC(a-b, b)

  2. PGDC(a, a) = a
Exemple de calcul de PGDC(42, 24):
  1. 42 > 24, alors PGDC(42, 24) = PGDC(42--24, 24) = PGDC(18, 24) = PGDC(24,18)

  2. 24 > 18, alors PGDC(24, 18) = PGDC(24--18, 18) = PGDC(6, 18) = PGDC(18, 6)

  3. 18 > 6, alors PGDC(18, 6) = PGDC(18--6, 6) = PGDC(12, 6)

  4. 12 > 6, alors PGDC(12, 6) = PGDC(12--6, 6) = PGDC(6, 6)

  5. Résultat: PGDC(42, 24) = PGDC(6, 6) = 6
Indication: utilisez une boucle (par exemple while) qui s'occupe de modifier et de tester les valeurs de a et b jusqu'à ce qu'une solution soit trouvée.

Exercice 9: Permutations et combinaisons (Algorithme, if, boucles, Niveau 2)

Complétez le programme fourni CombiPermu.java

Commencez par le coder de façon simple puis réfléchissez à une solution permettant de réduire le nombre de calculs redondants.


Exercice 10: Rebonds de balles (for, do while, Niveau 2)

Cours d'Informatique - Série 4

Première partie

Objectif :

L'objectif de cet exercice est de résoudre le problème suivant :

Lorsqu'une balle tombe d'une hauteur initiale h, sa vitesse à l'arrivée au sol est v=sqrt(2*h*g). Immédiatement après le rebond, sa vitesse est v1=eps*v (où eps est une constante et v la vitesse avant le rebond). Elle remonte alors à la hauteur h=(v1*v1)/(2*g).

Le but est d'écrire un programme (Rebonds1.java) qui calcule la hauteur à laquelle la balle remonte après un nombre nbr de rebonds.

Méthode :

On veut résoudre ce problème, non pas du point de vue formel (équations) mais par simulation du système physique (la balle).

Utilisez une itération for et des variables v, v1, (les vitesses avant et après le rebond), et h, h1 (les hauteurs au début de la chute et à la fin de la remontée).

Tâches :

Écrivez le programme Rebonds1.java qui affiche la hauteur après le nombre de rebonds spécifié.

Votre programme devra utiliser la constante g, de valeur 9,81 et demander à l'utilisateur d'entrer les valeurs de :

Essayez les valeurs H0 = 25, eps = 0.9, NBR = 10. La hauteur obtenue devrait être environ 3.04.

Deuxième partie

On se demande maintenant combien de rebonds fait cette balle avant que la hauteur à laquelle elle rebondit soit plus petite que (ou égale à) une hauteur donnée h_fin.

Écrivez le programme Rebonds2.java qui affiche le nombre de rebonds à l'écran.

Il devra utiliser une boucle do...while, et demander à l'utilisateur d'entrer les valeurs de :

Essayez les valeurs H0=10, eps=0.9 et h_fin=2.Vous devriez obtenir 8 rebonds.

Exercice 11: MOOC (cours en ligne) (MOOC, Niveau 2)

Les devoirs du MOOC, même s'il ne sont pas notés pour vous, sont un bon moyen de vous entraîner aussi. Vous pouvez les soumettre à un correcteur automatique (autant de fois que vous le souhaitez) et recevoir un feedback. Depuis cette semaine, vous disposez de suffisamment d'outils pour aborder le devoir de la semaine 2 et le devoir de la semaine 3, où il sera question de champignons, de location de vélos et de parachutes ;-)

Exercice 12: Eclipse Tutorial 6 (inutile si vous travaillez avec IntelliJ): Utilisation d'un dévermineur (Eclipse, Niveau 0)

Intégrez le fichier Newton.java dans votre répertoire de travail, par exemple [chemin vers le workspace]/Serie03/src et intégrez-le dans le projet Eclipse correspondant. Le programme Newton.java permet de calculer la racine carrée d'un nombre au moyen de l'algorithme de Newton. Commençons par décrire le fonctionnement de ce petit algorithme. Soit x la racine carrée d'un nombre n. On choisit une valeur comme approximation de départ pour x (1 dans le cas du programme fourni), puis on applique la formule de récurrence suivante :

xk+1 = 1/2 *(xk + n/xk)

Cette formule s'applique, jusqu'à ce que :

Dans le programme fourni, et pour simplifier un peu les choses, c'est le premier type de condition d'arrêt qui est choisi (avec 10 itérations) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
 
import java.util.Scanner;

/**
 * Newton
 * 
 * A small utility that computes the square root of a number using newtons algorithm.
 * 
 * The formula for the element x(k + 1) is (1/2)*(x(k) + n/x(k))
 * 
 * Usually, the algorithm is ended after a certain precision is reached or the result
 * changes very little. To keep this example simple, we will stick to a fixed number
 * of iterations (10 in this example).
 */
public class Newton {
    private static Scanner scanner = new Scanner(System.in);

    public static void main(String[] args) {
        System.out.println("Please enter the number: ");
        double value = scanner.nextDouble();
        
        //initial value x0 = 1
        double x = 1;
        for (int i = 0; i < 10; i++) {
            //calculate next value
            x = (1/2) * (x + value / x);
        }
        
        System.out.println("The square root of " + value + " is " + x);
    }

}

Lancez le programme et essayez-le pour le nombre 2.0 :

Hum... la valeur calculée est NaN (Not a Number), ce qui est clairement incorrect !

Comme le programme "compile" et qu'aucun message d'erreur n'est généré, nous n'avons, à ce stade, aucune indication sur la source de l'erreur. Il nous faut donc examiner le programme d'un peu plus près pour essayer de localiser le problème : cette tâche ingrate porte des noms parlants tels que "déverminage", "deboggage" (ou "debugging" le plus souvent !).

Une première façon de déverminer consiste à insérer, à des endroits pertinents, du code affichant des informations sur le déroulement du programme et les valeurs des différentes variables (par exemple System.out.println(x)). C'est la méthode que l'on utiliserait si l'on programmait au moyen d'un éditeur de texte basique. Autant dire les choses clairement, c'est en général laborieux; d'autant plus qu'il faut ensuite "nettoyer" le code de toutes instructions "parasites" liées au déverminage.

Seconde option, utiliser un outil dédié à ce genre de tâche : soit un dévermineur (debugger). Ce tutorial a pour but de vous apprendre à utiliser le dévermineur intégré à Eclipse.

Au moyen du bouton droit de la souris, cliquez sur le programme Newton.java dans la vue "Navigator" et choisissez l'option "Debug As -> 1 Java Application".

Le programme va démarrer son exécution, un nombre va vous être demandé et le prosaique NaN de tout à l'heure va à nouveau s'afficher. En fait, tout se passe comme si on avait lancé le programme avec l'option "Run As". Mais pourquoi donc ?

En fait, un dévermineur a besoin d'être informé un minimum de ce que vous souhaitez examiner. En clair, il fonctionne au moyen de "points d'arrêt" (Breakpoints) que vous aurez vous même définis. Les "breakpoints" sont des endroits dans votre programme à partir desquels vous souhaitez arrêter le déroulement normal de l'exécution pour examiner de plus près ce qui se produit. Nous avons donc besoin de définir au moins un "breakpoint".

Comme on ne sait pas trop où l'erreur se situe (et que notre progamme est de petite taille), choisissons de le placer au niveau de la première instruction de notre méthode main. Concrètement : il faut vous placer dans l'éditeur de Eclipse et cliquer au moyen du bouton droit de la souris dans la marge gauche (juste à gauche de la ligne verticale grise). Faites ceci au niveau de de la première instruction de la méthode main. Dans le menu qui apparaîtra alors, sélectionnez l'option "Toggle Breakpoint".

 

Un petit point bleu apparaîtra alors, signalant le point d'arrêt.

Lancez maintenant le programme une nouvelle fois au moyen de l'option "Debug As -> Java Application". Lorsque le point d'arrêt sera atteint, Eclipse vous demandera de basculer vers une perspective "Debug" (note : une perspective est un ensemble de vues cohérentes qui permet de travailler sur un sujet).

Sélectionnez "Remember my decision" et cliquez sur "Yes".

Vous vous trouvez maintenant dans la perspective "Debug"; ce qui devrait ressembler à ceci :

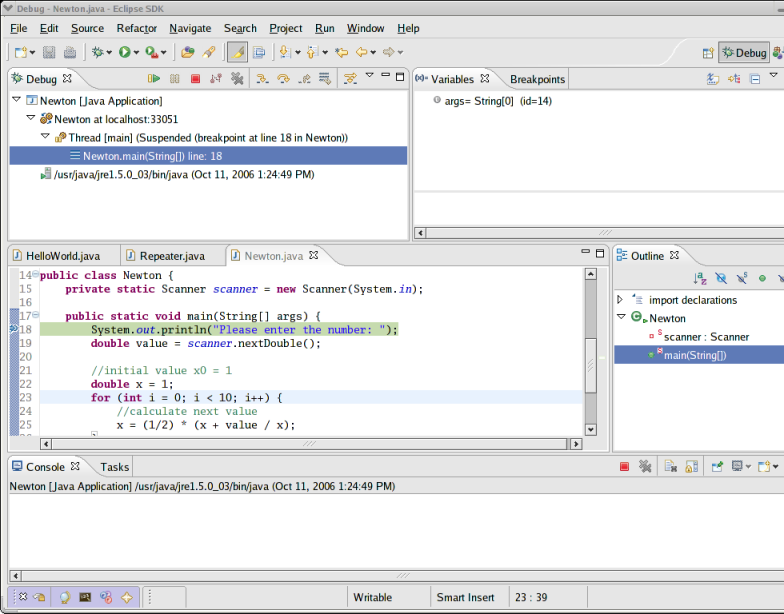
Pour comprendre ce que vous voyez, Il est nécessaire de savoir un minimum de chose sur une des techniques classiques du déverminage , à savoir :

Au milieu de l'écran, vous pouvez voir une fenêtre éditeur dans laquelle une ligne de code est mise en évidence :

Il s'agit de la ligne sur laquelle l'exécution du programme est positionnée.

Vous pouvez maintenant utiliser la barre à outils :

pour contrôler l'exécution de votre programme. Déplacez votre souris sur les différents boutons (en y restant quelques secondes) pour voir les différentes options utilisables. Nous vous décrivons ci-dessous les options les plus importantes. Notez que celles qui sont relatives aux méthodes ne vous seront utiles qu'à partir du cours sur la modularisation, dans deux semaines, si vous suivez la progression du cours. Voici donc les quelques options les plus utiles 

"Resume": permet de quitter le mode "Pas à Pas" et continue l'exécution jusqu'au prochain point d'arrêt.
"Step Into": Si la ligne courante correspond à un appel de méthode, on "entre" dans le corps de cette méthode pour examiner pas à pas son fonctionnement
"Step Over": sauter à la prochaine ligne. Si la ligne courante correspond à un appel de méthode, on exécute l'appel à la méthode sans examiner l'exécution de son corps

Vous pouvez voir, en haut à droite, la vue "Variables" où s'affichent les variables et leurs valeurs dans les différents contextes d'exécution :

Utilisez maintenant le bouton "Step Over" pour poursuivre l'exécution de tout le programme. Gardez un oeil sur la variable x et n'oubliez pas d'entrer une valeur dans la console lorsque le programme vous la demandera (ligne 16).

Vous remarquerez alors que x prend la valeur 0 à la première itération, puis NaN à la suivante. Le calcul :

x = (1/2) * (x + value / x)

retourne donc zéro quand x vaut 1 et value vaut 2.0. Vos connaissances arithmétiques vous dirons que pour qu'une multiplication vaille 0, il faut qu'un moins l'un des opérandes soit nul. Ici :

(1/2) est clairement non-nul,

c'est donc x + value / x qui l'est (... étrange vu que x vaut 1 et value vaut 2 !)

Si nous examinons cette expression, on peut remarquer en fait que la division effectuée est une division entière. Ce qui en effet retourne bien zéro. Nous pouvons corriger ce problème en travaillant avec des valeurs de type double :

Exécutez une nouvelle fois le programme après correction :

cette fois tout fonctionne correctement.


Exercice 13: IntelliJ Tutorial 5: Utilisation d'un dévermineur (IntelliJ, Niveau 0)

Intégrez le fichier Newton.java dans votre répertoire de travail, par exemple [chemin vers le workspace IntelliJ]/Serie03/src et intégrez-le dans le projet IntelliJ correspondant. Le programme Newton.java permet de calculer la racine carrée d'un nombre au moyen de l'algorithme de Newton. Commençons par décrire le fonctionnement de ce petit algorithme. Soit x la racine carrée d'un nombre n. On choisit une valeur comme approximation de départ pour x (1 dans le cas du programme fourni), puis on applique la formule de récurrence suivante :

xk+1 = 1/2 *(xk + n/xk)

Cette formule s'applique, jusqu'à ce que :

Dans le programme fourni, et pour simplifier un peu les choses, c'est le premier type de condition d'arrêt qui est choisi (avec 10 itérations) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
 
import java.util.Scanner;

/**
 * Newton
 * 
 * A small utility that computes the square root of a number using newtons algorithm.
 * 
 * The formula for the element x(k + 1) is (1/2)*(x(k) + n/x(k))
 * 
 * Usually, the algorithm is ended after a certain precision is reached or the result
 * changes very little. To keep this example simple, we will stick to a fixed number
 * of iterations (10 in this example).
 */
public class Newton {
    private static Scanner scanner = new Scanner(System.in);

    public static void main(String[] args) {
        System.out.println("Please enter the number: ");
        double value = scanner.nextDouble();
        
        //initial value x0 = 1
        double x = 1;
        for (int i = 0; i < 10; i++) {
            //calculate next value
            x = (1/2) * (x + value / x);
        }
        
        System.out.println("The square root of " + value + " is " + x);
    }

}

Lancez le programme et essayez-le pour le nombre 2.0 (ou 2,0 selon vos "Locales", voir à ce propos la note en bas de l'exercice 2.8) :

Hum... la valeur calculée est NaN (Not a Number), ce qui est clairement incorrect !

Comme le programme "compile" et qu'aucun message d'erreur n'est généré, nous n'avons, à ce stade, aucune indication sur la source de l'erreur. Il nous faut donc examiner le programme d'un peu plus près pour essayer de localiser le problème : cette tâche ingrate porte des noms parlants tels que "déverminage", "deboggage" (ou "debugging" le plus souvent !).

Une première façon de déverminer consiste à insérer, à des endroits pertinents, du code affichant des informations sur le déroulement du programme et les valeurs des différentes variables (par exemple System.out.println(x)). C'est la méthode que l'on utiliserait si l'on programmait au moyen d'un éditeur de texte basique. Autant dire les choses clairement, c'est en général laborieux; d'autant plus qu'il faut ensuite "nettoyer" le code de toutes instructions "parasites" liées au déverminage.

Seconde option, utiliser un outil dédié à ce genre de tâche : soit un dévermineur (debugger). Ce tutorial a pour but de vous apprendre à utiliser le dévermineur intégré à IntelliJ.

Au moyen du bouton droit de la souris, cliquez sur le programme Newton.java dans la vue "Navigator" et choisissez l'option "Debug 'Newton.main()'".

Le programme va démarrer son exécution, un nombre va vous être demandé et le prosaique NaN de tout à l'heure va à nouveau s'afficher. En fait, tout se passe comme si on avait lancé le programme avec l'option "Run As". Mais pourquoi donc ?

En fait, un dévermineur a besoin d'être informé un minimum de ce que vous souhaitez examiner. En clair, il fonctionne au moyen de "points d'arrêt" (Breakpoints) que vous aurez vous même définis. Les "breakpoints" sont des endroits dans votre programme à partir desquels vous souhaitez arrêter le déroulement normal de l'exécution pour examiner de plus près ce qui se produit. Nous avons donc besoin de définir au moins un "breakpoint".

Comme on ne sait pas trop où l'erreur se situe (et que notre progamme est de petite taille), choisissons de le placer au niveau de la première instruction de notre méthode main. Concrètement : il faut vous placer dans l'éditeur de IntelliJ et cliquer dans la marge à gauche (juste à gauche de la ligne verticale grise) juste avant la ligne de code en question. Faites ceci au niveau de de la première instruction de la méthode main. Un petit point rouge apparaîtra alors, signalant le point d'arrêt.

 

Lancez maintenant le programme une nouvelle fois au moyen de l'option "Debug 'Newton.main()'". Vous devriez arriver dans une perspective "Debug" (note : une perspective est un ensemble de vues cohérentes qui permet de travailler sur un sujet).

Vous vous trouvez maintenant dans la perspective "Debug"; ce qui devrait ressembler à ceci :

Pour comprendre ce que vous voyez, Il est nécessaire de savoir un minimum de chose sur une des techniques classiques du déverminage , à savoir :

Au milieu de l'écran, vous pouvez voir une fenêtre éditeur dans laquelle une ligne de code est mise en évidence :

Il s'agit de la ligne sur laquelle l'exécution du programme est positionnée.

Vous pouvez maintenant utiliser la barre à outils :

pour contrôler l'exécution de votre programme. Déplacez votre souris sur les différents boutons (en y restant quelques secondes) pour voir les différentes options utilisables. Nous vous décrivons ci-dessous les options les plus importantes. Notez que celles qui sont relatives aux méthodes ne vous seront utiles qu'à partir du cours sur la modularisation, dans deux semaines, si vous suivez la progression du cours. Voici donc les quelques options les plus utiles 

"Resume": permet de quitter le mode "Pas à Pas" et continue l'exécution jusqu'au prochain point d'arrêt.
"Step Into": Si la ligne courante correspond à un appel de méthode, on "entre" dans le corps de cette méthode pour examiner pas à pas son fonctionnement
"Step Over": sauter à la prochaine ligne. Si la ligne courante correspond à un appel de méthode, on exécute l'appel à la méthode sans examiner l'exécution de son corps

Vous pouvez voir, en bas à droite, la vue "Variables" dans l'onglet debugger où s'affichent les variables et leurs valeurs dans les différents contextes d'exécution :

Utilisez maintenant le bouton "Step Over" pour poursuivre l'exécution de tout le programme. Gardez un oeil sur la variable x et n'oubliez pas d'entrer une valeur dans la console lorsque le programme vous la demandera (ligne 16).

Vous remarquerez alors que x prend la valeur 0 à la première itération, puis NaN à la suivante. Le calcul :

x = (1/2) * (x + value / x)

retourne donc zéro quand x vaut 1 et value vaut 2.0. Vos connaissances arithmétiques vous dirons que pour qu'une multiplication vaille 0, il faut qu'un moins l'un des opérandes soit nul. Ici :

(1/2) est clairement non-nul,

c'est donc x + value / x qui l'est (... étrange vu que x vaut 1 et value vaut 2 !)

Si nous examinons cette expression, on peut remarquer en fait que la division effectuée est une division entière. Ce qui en effet retourne bien zéro. Nous pouvons corriger ce problème en travaillant avec des valeurs de type double :

Exécutez une nouvelle fois le programme après correction :

cette fois tout fonctionne correctement.


Dernière mise à jour: 27/09/2024  (Revision: 1.2)